Pascal was talking about the bet in the context of if one should believe in the existence of god (or not).
It has been applied to the debate on climate change recently.
Here, this serves as an introduction to what follows.
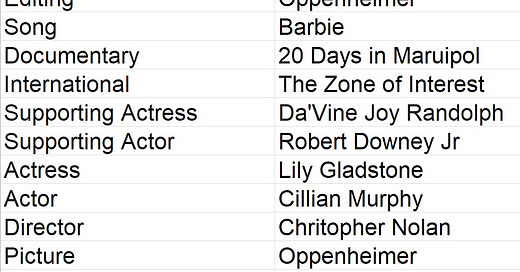
I have a hobby horse: Guessing Oscar Winners. I have been at it for two decades.
This was my choice card this year.
Yes, it was produced a week before the ceremony happened.
https://www.linkedin.com/feed/update/urn:li:activity:7170580247979962369/
This year, my score is 11 out of 12. [Loss of Gladstone was a great disappointment.]
Executive question: What are the chances of getting 11 out of 12 right?
[There are five nominees in each category except for the Best Picture.
The best movie has 10 possible choices - we ignore that in my discussion below.]
Suppose I take all trials independent (they really are not - but we ignore that for now).
It simplifies what follows. With that assumption, I can then use a Binomial distribution with n=12
The probability of getting one right is 0.2 (one out of five).
Here we can calculate the chance of success
P(At least 11 out of 12) = 0.0000002.
[There are six zeros before that 2]
Full calculation:
Suppose I have better priors and improve my chance
to 0.5 (rather than 0.2)
Then P(At least 11 out of 12) = 0.003.
That improves the result but it is still 3 out of 1,000.
Executive result: It is not easy to guess 11 out of 12 right even for better odds.
Executive question: If you want to raise the probability of right answers, with P(At least 11 out of 12) = 0.5, what would you need to raise the individual probabilities to be?
Executive answer: 0.9. [I will leave it as a finger exercise how I got that.]
Executive question: How does one make these guesses? If you really like a movie or an actor or a song, does it count? Not at all. You have to guess what the voting members of the Academy would like. This process is very much like the guessing the beauty contest winners that Keynes talked about.
Executive digression: Oscars versus Grammys. Voting for Grammys is different today. You rank order your preference. This change was executed by a Finnish American economist. He has some interesting stories about the Afterparty at the Grammys!
Executive conclusion: To get better than even odds, you really really need to know what you are doing.
You don't have to take my word for the executive conclusion.
It shows up in the betting pools.
I have bet $800.
The winning pool stands at around $40,000 right now. It will divided up among the winners. Like every year, *all* my winnings go to charity. [This year, to an orphanage in Mexico. To the children whose parents died of HIV/AIDS whom the relative have rejected.]
So, even among the bettors (presumably experts), the chance of getting 11 out of 12 right is 1/50 [800/40,000].
That means they have raised the probability of individual category win WAY above 0.5.
Obviously I will not get $40,000. It will take some time before they tell us how many winners there are and then how much each would get (they verify a few things like a confirmation that you are not a member of the Academy).
Executive teaching moment: It is a good (somewhat simplified) exercise on how the humble Binomial distribution can be applied in real life.